Números racionales
Los números racionales son aquellos que se pueden expresar como el cociente entre un número entero a y un número natural b (recordemos que consideramos a los números naturales como números enteros positivos).
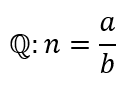
Los números racionales se dividen en:
- Números enteros: aquellos con b=1 o fracciones equivalentes. Por ejemplo: a=2 y b=1 es equivalente a a=4 y b=2. El conjunto de números enteros forma parte del conjunto de números racionales, por tanto, los números enteros son siempre racionales, sin embargo, los números racionales no son necesariamente enteros.
- Números fraccionarios: también llamadas fracciones. Están formados por un numerador a y un denominador b. Como las fracciones representan una división; si realizamos esta división nos aparecerán números racionales en base decimal. Los números racionales con parte decimal se clasifican en 3 tipos:
- Números decimales exactos: son aquellos que tienen un número de cifras en su parte decimal finito (es decir, que se puede contar). Veamos ejemplos:
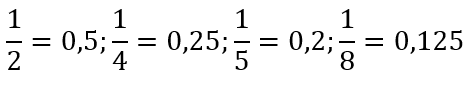
2. Números periódicos: son aquellos que tienen un número infinito de cifras en su parte decimal (es decir, un número incontable de cifras que no se 'acaba'). Se clasifican en dos tipos:
- Números periódicos puros: aquellos que inmediatamente en la parte decimal del número tiene una o más cifras que se repiten continuamente hasta el infinito. Veamos ejemplos:
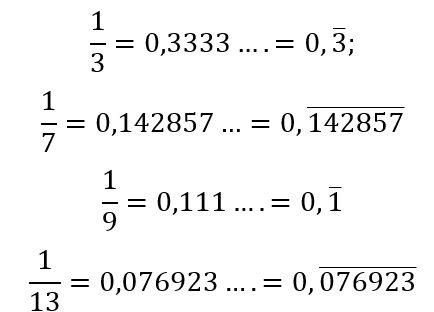
- Números periódicos mixtos: aquellos que en la parte decimal tienen, antes de la parte periódica, una o más cifras que no se repiten. Ejemplos:

NOTA: Los 'sombreritos' encima de una o más cifras decimales indica qué cifras se repiten.
Por último, si representamos en una recta los números racionales, tenemos:

