Números complejos

Los números complejos son aquellos que se expresan como la suma de un número real y un número imaginario (que es un múltiplo real de i, que veremos a continuación):

Algunas veces, al hacer la raíz cuadrada de un número negativo en la calculadora, hemos podido ver que nos indicaba que había un error matemático, pues en el conjunto de los números reales, no hay solución posible. Por ello, se definen los números imaginarios. Veamos un ejemplo:

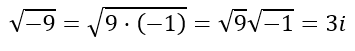
En esta entrada, no realizaremos operaciones con números complejos y nos centraremos únicamente en su definición.

El lector, con lo expuesto anteriormente, podría preguntarse si los números reales son números complejos. La respuesta es SÍ, los números reales son números complejos con parte imaginaria nula, es decir (teniendo en cuenta nuestra notación), b=0.

Por su parte, los números imaginarios también son números complejos con parte real nula, es decir, a=0.

Veamos ejemplos de números complejos:

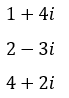
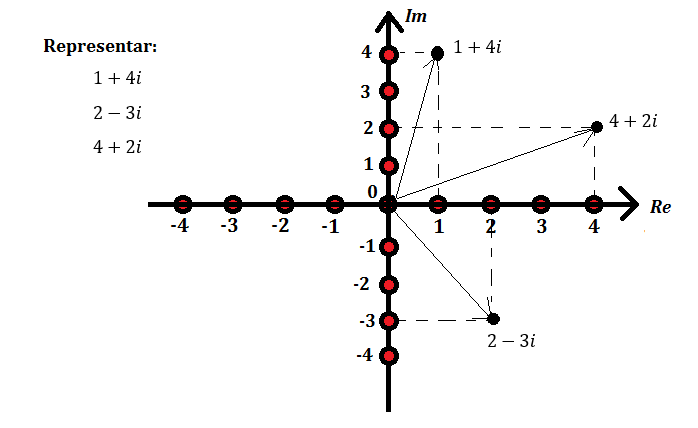
Por último, veremos la representación de los números complejos. Anteriormente, hemos visto como los números reales siempre se representaban en una recta infinita. Sin embargo, esto no ocurre con los números complejos al haber dos partes diferenciadas (real e imaginaria). Veámoslo representando los 3 ejemplos anteriores. Para hacerlo, necesitaremos un plano complejo. El eje de ordenadas (vertical) servirá para representar la parte imaginaria, y el eje de abscisas (horizontal) hará lo propio con la parte real.

La parte imaginaria se expresa como 'Im' y la parte real como 'Re'. Así, para un número complejo z=a+bi, Re(z)=a y Im(z)=b.

Con esto, representemos los 3 ejemplos de números complejos anteriores: