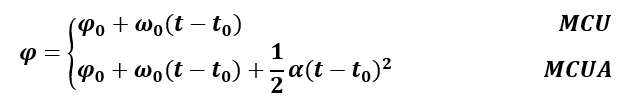Movimiento curvilíneo: MCU y MCUA
Movimiento curvilíneo es todo aquel cuya trayectoria no describa una línea recta. En la vida cotidiana, este tipo de movimientos es más frecuente que el rectilíneo y se da, por ejemplo, en el movimiento que describen los planetas alrededor del Sol (OJO: estas trayectorias son elípticas no circulares) o en la trayectoria parabólica que sigue un balón al ser golpeado.
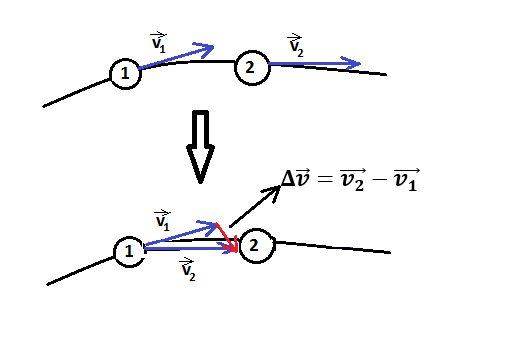
Atendiendo a la resta de vectores podemos hallar el vector diferencia entre las velocidades. Recordemos la definición de aceleración:
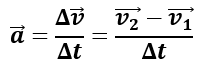
Como la aceleración es el cociente entre una magnitud vectorial (vector diferencia de velocidades) y una escalar (el tiempo), recordando las propiedades de los vectores, entonces tenemos que el vector aceleración tendrá la misma dirección y sentido que el vector diferencia de velocidades (lo único que cambiará será el módulo del vector en función del tiempo):
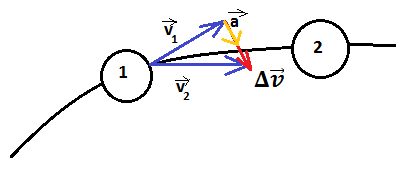
El vector aceleración es el vector amarillo, mientras que el vector diferencia de velocidades es el vector rojo. Si consideramos el sistema cartesiano (ejes x e y), podemos descomponer el vector aceleración:
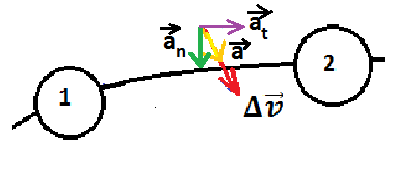
Mientras que la aceleración tangencial indica el cambio en el módulo del vector velocidad, la aceleración normal indica el cambio en la dirección de la velocidad. Veamos cómo se calculan cada una de ellas sabiendo que en un movimiento curvilíneo existe una curvatura de radio R.
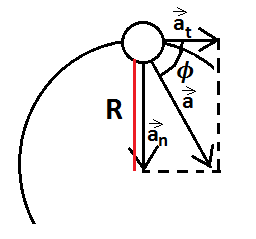
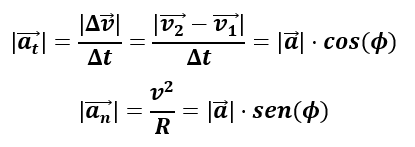
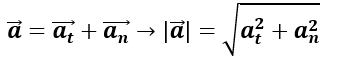
Para el caso de un movimiento circular, el radio de la curvatura siempre es el mismo. A continuación estudiaremos este movimiento:
Movimiento circular: MCU y MCUA
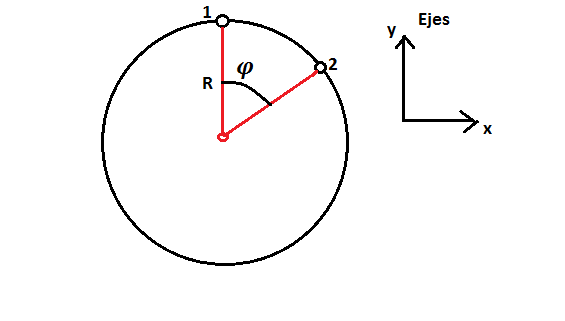
En primer lugar, tenemos que hallar el desplazamiento de un cuerpo que se mueve desde la posición 1 hasta la posición 2. Tendremos que el vector desplazamiento vendrá dado por:

Recordemos que la curvatura en un movimiento circular es siempre la misma. Sabiendo esto, hallaremos los vectores velocidad y aceleración:
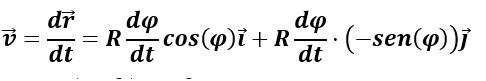
El vector velocidad es simplemente la derivada respecto al tiempo del vector desplazamiento. En cuanto al vector aceleración, este será la derivada respecto al tiempo del vector velocidad:
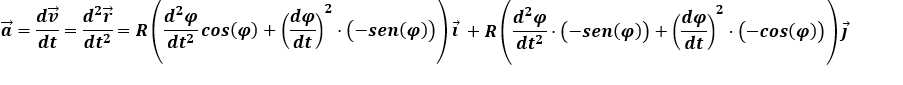
Sabiendo que la velocidad angular es la variación del ángulo girado durante un tiempo, por tanto:
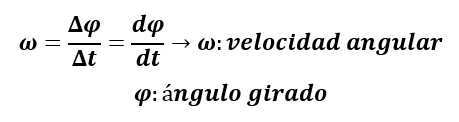
Por otra parte, la aceleración angular indica la variación de la velocidad angular en función del tiempo:
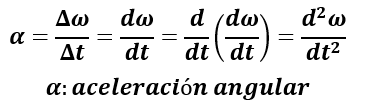
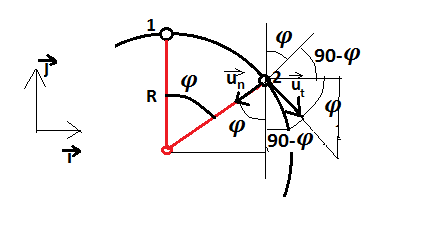
A continuación, vamos a definir vectores unitarios en las direcciones tangencial y normal (perpendicular) al movimiento, en lugar de en las direcciones de los ejes x e y:
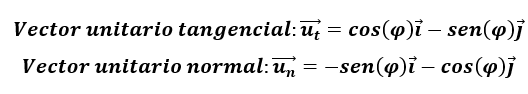
Sabiendo esto, redefinimos los vectores velocidad, desplazamiento y aceleración en función de estos vectores unitarios y obtenemos:
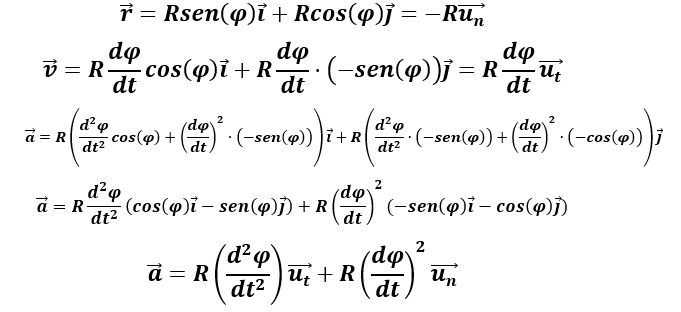
Si además sustituimos la aceleración y velocidad angular en cada uno de los vectores, tenemos:

Veamos que los módulos de la aceleración normal y tangencial coinciden con los indicados anteriormente. En primer lugar, tenemos que el módulo de la velocidad es:
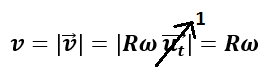
Recordemos que el módulo de un vector unitario es 1. Sabiendo ahora la relación entre el módulo de la velocidad y la velocidad angular, hallamos los módulos de la aceleración tangencial y normal:
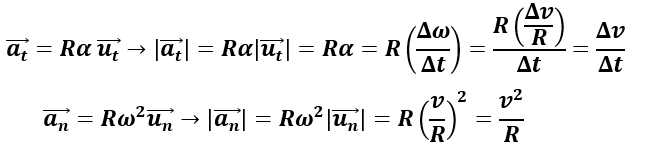
De nuevo recordemos que el módulo de los vectores unitarios es uno. Como podemos comprobar, los módulos de la aceleración normal y tangencial son los enunciados previamente.
A continuación estudiaremos las ecuaciones para un movimiento circular uniformemente acelerado (MCUA) y un movimiento circular uniforme (MCU).
En primer lugar, la aceleración angular para cada movimiento será:
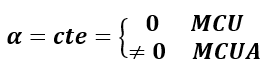
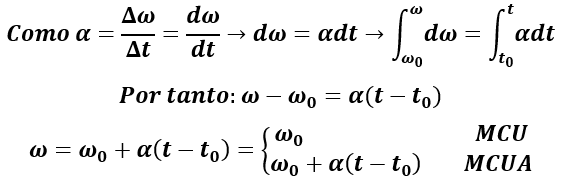
Estas últimas son las ecuaciones de la velocidad angular para un MCU (aceleración angular 0) y un MCUA (aceleración angular constante y distinta de cero). En cuanto a las ecuaciones del ángulo girado tenemos:
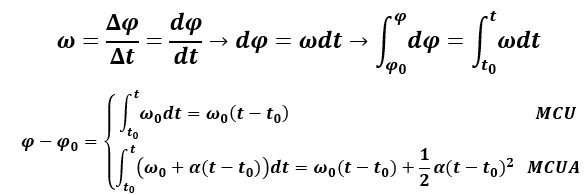
Por tanto, las ecuaciones para el ángulo girado serán (para un MCU y un MCUA):