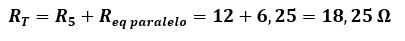Circuito mixto
Un circuito mixto es aquel que tiene elementos del mismo conectados en serie y otros conectados en paralelo. Para resolverlo, debemos analizar las distintas partes del circuito y utilizar las fórmulas que procedan en función de si la parte del circuito en cuestión tiene conexiones en serie o en paralelo.
Veamos un ejemplo:
EJEMPLO 1: Para el circuito de la figura, calcular:
a) Resistencia equivalente del circuito.
b) Voltaje en cada una de las resistencias.
c) Intensidad en cada una de las resistencias.

En primer lugar, antes de resolverlo, analizamos el circuito por partes. Nos preguntaremos, ¿coinciden los terminales de entrada y salida de los elementos del circuito o dichos elementos se conectan sucesivamente?
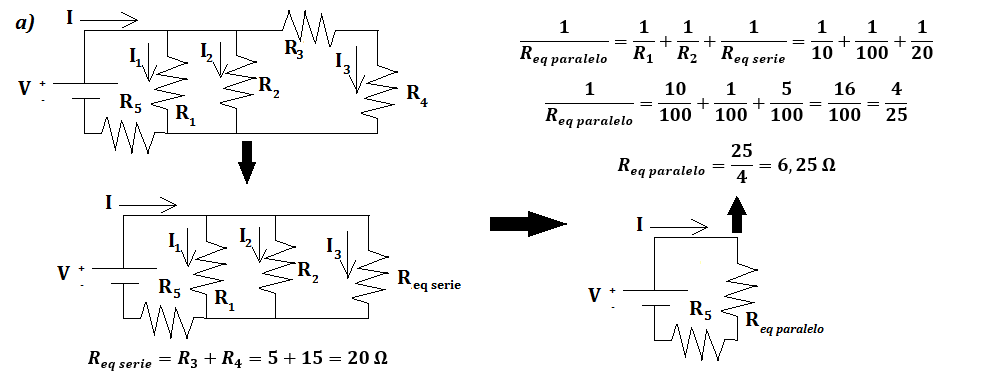
Vemos claramente que las resistencias 3, 4 y 5 se conectan sucesivamente, es decir, en serie. Veamos cuál es la resistencia equivalente a estas 3:
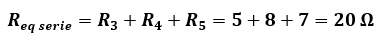
Como vemos nos queda un circuito en paralelo. Hallamos ahora la resistencia equivalente total del circuito:
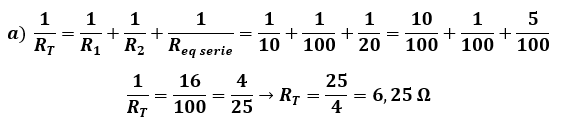
Ahora, en el apartado b, nos piden hallar el voltaje en cada una de las resistencias. Para ello vayámonos primero al circuito paralelo (el voltaje es el mismo porque coinciden los terminales de las resistencias) que sale de hallar la resistencia equivalente de la asociación de las resistencias 3, 4 y 5.

Por último, calculamos las intensidades en cada parte del circuito (ya tenemos la intensidad que circula por las resistencias 3, 4 y 5 del apartado anterior):

En resumen, la estrategia para realizar un circuito mixto, es separarlo en partes, y en función de si los elementos de esta parte se conectan en serie o en paralelo, lo resolvemos de una forma u otra.
Veamos otro ejemplo:
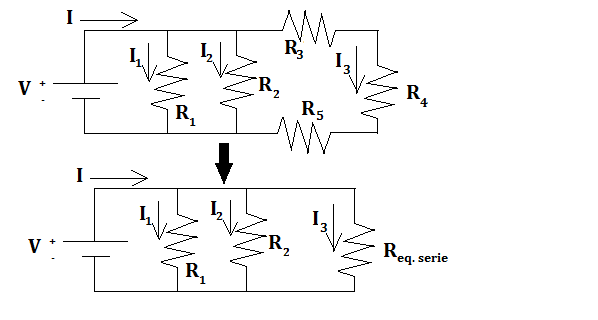
EJEMPLO 2: Resolver los mismos apartados que en el ejemplo anterior para el circuito de la figura:
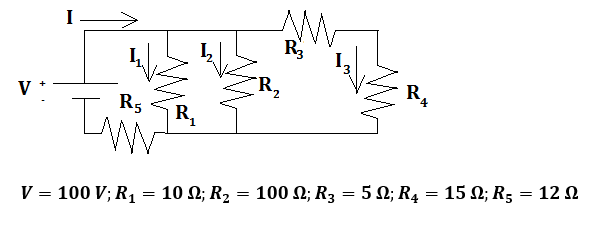
En primer lugar, para hallar la resistencia equivalente del circuito, hallamos la resistencia equivalente de la asociación de las resistencias 3 y 4. A continuación nos queda esta resistencia equivalente en paralelo con las resistencias 1 y 2, calculamos la resistencia equivalente en paralelo de estas 3 mencionadas.
Por último, esta resistencia equivalente queda en serie con la resistencia 5. Hallamos la resistencia equivalente de este circuito en serie y tendremos la resistencia equivalente total del circuito. Veámoslo: